Homotopy between composites of homotopic loops: Difference between revisions
No edit summary |
|||
| (3 intermediate revisions by the same user not shown) | |||
| Line 24: | Line 24: | ||
We can think of <math>F</math> as <math>F_1 * F_2</math>. | We can think of <math>F</math> as <math>F_1 * F_2</math>. | ||
===Graphical version=== | |||
The pictures below describe the explicit construction. Note that the geometric shapes shown in these pictures can be thought of as the sources of the respective maps to <math>X</math>, with the additional caveat that the boundary vertical lines map to the point <math>x_0</math>. (The same pictures, without the collapse of boundaries, work to establish the [[homotopy between composites of homotopic paths]]). | |||
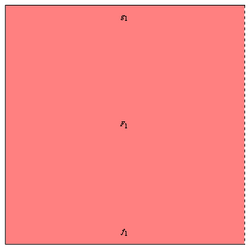
The homotopy <math>F_1</math> between <math>f_1</math> and <math>g_1</math> is a map from a filled unit square, where the restrictions of the map to the bottom and top sides of the square are <math>f_1</math> and <math>g_1</math> respectively. The left and right sides map to the point <math>x_0</math>: | |||
[[File:Homotopyleftofcomposition.png|250px]] | |||
The homotopy <math>F_2</math> between <math>f_2</math> and <math>g_2</math> is a map from a filled unit square, where the restrictions of the map to the bottom and top sides of the square are <math>f_2</math> and <math>g_2</math> respectively. The left and right sides map to the point <math>x_0</math>: | |||
[[File:Homotopyrightofcomposition.png|250px]] | |||
These homotopies are composed by concatenation, as shown below. Both <math>F_1</math> and <math>F_2</math> need to be scaled by a factor of <math>1/2</math> for the concatenated homotopy to fit in a unit square: | |||
[[File:Homotopyofcompositepaths.png|250px]] | |||
Latest revision as of 18:45, 18 December 2010
Statement
Existential version
Suppose is a topological space, is a point in , and are loops based at with the property that is homotopic to (as a loop based at ) and is homotopic to (again, as a loop based at ). Then, is homotopic to .
Constructive/explicit version
More explicitly, suppose is a homotopy from to . In other words, is a continuous map (where is the circle, viewed as with endpoints identified, and is the closed unit interval) having the following properties:
- (here is the chosen basepoint of the circle from which we're mapping). This says that the loop always remains based on .
Similarly, suppose is a continuous map having the following properties:
- (here is the chosen basepoint of the circle). This says that the loop always remains based on .
Then, we can consider the following homotopy from to :
We can think of as .
Graphical version
The pictures below describe the explicit construction. Note that the geometric shapes shown in these pictures can be thought of as the sources of the respective maps to , with the additional caveat that the boundary vertical lines map to the point . (The same pictures, without the collapse of boundaries, work to establish the homotopy between composites of homotopic paths).
The homotopy between and is a map from a filled unit square, where the restrictions of the map to the bottom and top sides of the square are and respectively. The left and right sides map to the point :
The homotopy between and is a map from a filled unit square, where the restrictions of the map to the bottom and top sides of the square are and respectively. The left and right sides map to the point :
These homotopies are composed by concatenation, as shown below. Both and need to be scaled by a factor of for the concatenated homotopy to fit in a unit square:












![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
![{\displaystyle I=[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87ec65159c44769434523e46928bc1b82681f842)