Statement
Existential version
Suppose  is a topological space,
is a topological space,  is a point in
is a point in  , and
, and  are loops based at
are loops based at  with the property that
with the property that  is homotopic to
is homotopic to  (as a loop based at
(as a loop based at  ) and
) and  is homotopic to
is homotopic to  (again, as a loop based at
(again, as a loop based at  ). Then,
). Then,  is homotopic to
is homotopic to  .
.
Constructive/explicit version
More explicitly, suppose  is a homotopy from
is a homotopy from  to
to  . In other words,
. In other words,  is a continuous map (where
is a continuous map (where  is the circle, viewed as
is the circle, viewed as ![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d) with endpoints identified, and
with endpoints identified, and ![{\displaystyle I=[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87ec65159c44769434523e46928bc1b82681f842) is the closed unit interval) having the following properties:
is the closed unit interval) having the following properties:


 (here
(here  is the chosen basepoint of the circle from which we're mapping). This says that the loop always remains based on
is the chosen basepoint of the circle from which we're mapping). This says that the loop always remains based on  .
.
Similarly, suppose  is a continuous map having the following properties:
is a continuous map having the following properties:


 (here
(here  is the chosen basepoint of the circle). This says that the loop always remains based on
is the chosen basepoint of the circle). This says that the loop always remains based on  .
.
Then, we can consider the following homotopy from  to
to  :
:

We can think of  as
as  .
.
Graphical version
The pictures below describe the explicit construction. Note that the geometric shapes shown in these pictures can be thought of as the sources of the respective maps to  , with the additional caveat that the boundary vertical lines map to the point
, with the additional caveat that the boundary vertical lines map to the point  . (The same pictures, without the collapse of boundaries, work to establish the homotopy between composites of homotopic paths).
. (The same pictures, without the collapse of boundaries, work to establish the homotopy between composites of homotopic paths).
The homotopy  between
between  and
and  is a map from a filled unit square, where the restrictions of the map to the bottom and top sides of the square are
is a map from a filled unit square, where the restrictions of the map to the bottom and top sides of the square are  and
and  respectively. The left and right sides map to the point
respectively. The left and right sides map to the point  :
:
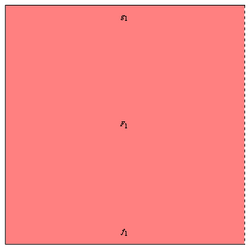
The homotopy  between
between  and
and  is a map from a filled unit square, where the restrictions of the map to the bottom and top sides of the square are
is a map from a filled unit square, where the restrictions of the map to the bottom and top sides of the square are  and
and  respectively. The left and right sides map to the point
respectively. The left and right sides map to the point  :
:

These homotopies are composed by concatenation, as shown below. Both  and
and  need to be scaled by a factor of
need to be scaled by a factor of  for the concatenated homotopy to fit in a unit square:
for the concatenated homotopy to fit in a unit square:













![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
![{\displaystyle I=[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87ec65159c44769434523e46928bc1b82681f842)















